The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
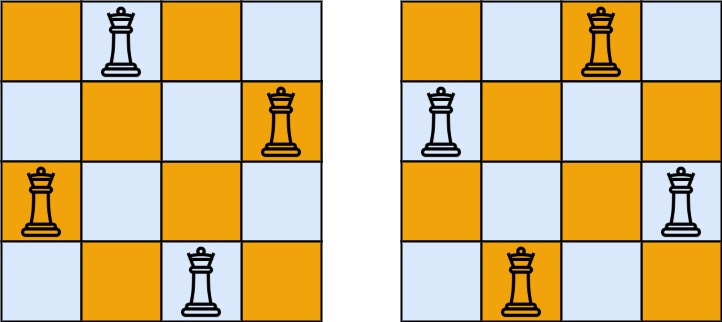
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Solution
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
col = set()
posDiag = set() # (r + c)
negDiag = set() # (r - c)
res = []
board = [["."] * n for i in range(n)]
def backtrack(r):
if r == n:
copy = ["".join(row) for row in board]
res.append(copy)
return
for c in range(n):
if c in col or (r + c) in posDiag or (r - c) in negDiag:
continue
col.add(c)
posDiag.add(r + c)
negDiag.add(r - c)
board[r][c] = "Q"
backtrack(r + 1)
col.remove(c)
posDiag.remove(r + c)
negDiag.remove(r - c)
board[r][c] = "."
backtrack(0)
return res

